单调栈 • Arshe's site

基础原理#

单调栈（Monotonic Stack）是一种特殊的栈结构，核心特点是：栈内元素始终保持单调递增 / 单调递减的顺序，通过在入栈时破坏单调性就弹出栈顶元素的规则，来维护栈的有序性。

栈内元素保持严格的单调性
新元素入栈时，会首先弹出所有不满足单调性的元素，再将新元素入栈

时间复杂度最优能到O(n)(每个元素最多入栈出栈一次)。栈内是否允许相等（严格/非严格）根据题目要求而定。

假设我们有数据流 [2, 1, 5, 6, 2, 3]，我们需要将他们加入单调递增的栈中。

过程如下：

栈为空，直接入栈 2
1 比 2 小，不满足单调性，弹出 2，入栈 1
5 比 1 大，满足单调性，入栈 5
6 比 5 大，满足单调性，入栈 6
2 比 6 小，不满足单调性，弹出 6，入栈 2
3 比 2 大，满足单调性，入栈 3

栈内最后剩余：[1, 2, 3]

应用场景#

解决 “下一个更大/更小元素” 问题#

题目：给定一个数组 nums，返回一个数组 answer，其中 answer[i] 是 nums[i] 右侧第一个比 nums[i] 大的元素。如果不存在这样的元素，answer[i] 为 -1。

输入： nums = [2, 1, 5, 6, 2, 3]

输出： [5, 5, 6, -1, 3, -1]

解题思路：

根据题目要求，我们需要找到右侧第一个比当前元素大的元素，因此我们需要维护一个单调递增栈
初始化栈为空，answer 数组为全 -1
遍历 nums 数组，对于每个元素 nums[i]：
- 若栈为空，直接入栈
- 若栈非空，比较栈顶元素与 nums[i]：
  - 若栈顶元素小于 nums[i]，则弹出栈顶元素，即当前栈顶元素的右侧第一个比它大的元素已找到。更新 answer[栈顶索引] 为 nums[i]，继续比较新的栈顶元素
  - 若栈顶元素大于等于 nums[i]，则 nums[i] 入栈（注意：这里允许相等，因为我们需要找到右侧第一个比它大的元素）

解题代码：

class Solution {
    public int[] nextGreaterElement(int[] nums) {
        int n = nums.length;
        int[] answer = new int[n];
        Arrays.fill(answer, -1);
        
        Deque<Integer> stack = new ArrayDeque<>(); // 存储元素索引，保持栈内元素索引对应的 nums 元素单调递增
        for (int i = 0; i < n; i++) {
            while (!stack.isEmpty() && nums[stack.peek()] < nums[i]) {
                answer[stack.pop()] = nums[i];
            }
            stack.push(i);
        }
        return answer;
    }
}

java

解决 “区间最值” 问题#

题目：给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。

输入：heights = [2,1,5,6,2,3]

输出：10

解释：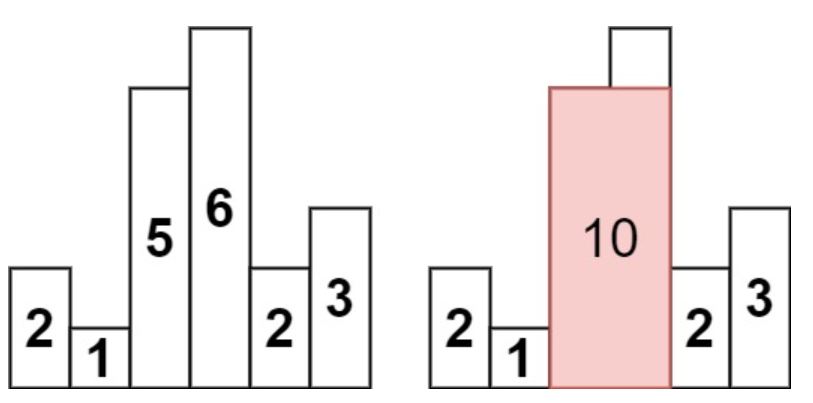

最大的矩形为图中红色区域，面积为 10

解题思路：

我们需要找出一个区间中，所能达到的最大高度，可记为h，这个区间的左右边界可记为l, r
创建一个栈，用于存储元素索引，保持栈内元素索引对应的 heights 元素单调递增
由于单调递增，栈顶元素的前一个一定是它的左边第一个比它小的元素，即为l
当栈顶元素出栈时，即找到了右边第一个它小的元素，当前元素的索引即为 r

以[ 2,1,5,6,2,3 ] 为例：

0(2) 进来，左边没有比它小的(可记为-1)，栈为0(2)
1(1) 想进来， 0(2)离开，则0(2)右边第一个比它小的是1(1) , 栈为空
1(1) 进来，左边没有比1(1)小的，栈为 1(1)
2(5) 想进来，直接进， 2(5) 左边第一个比它小的是进之前的栈顶1(1)，栈为 1(1), 2(5)
3(6) 想进来，直接进， 3(6)左边第一个比它小的是进之前的栈顶2(5)，栈为 1(1), 2(5), 3(6)
4(2) 想进来， 3(6)离开， 3(6)右边第一个比它小的是4(2)，栈为 1(1), 2(5)
2(5)离开， 2(5)右边第一个比它小的是4(2)，栈为 1(1),
4(2) 进来， 4(2)左边第一个比它小的是进之前的栈顶1(1)，栈为 1(1), 4(2)
5(3) 想进来，直接进， 5(3)左边第一个比它小的是进之前的栈顶 4(2)，栈为 1(1), 4(2), 5(3)

栈里剩余3个元素，说这3个元素往右没遇到比自己小的值，可记为n，也就是6

对于 0(2)，左-1，右1(1)，则(-1, 1)之前高度都能达到2，面积为 2 * (1 - (-1) - 1) = 2
对于 1(1)，左-1，右6，则(-1, 6)之前高度都能达到1，面积为 1 * (6 - (-1) - 1) = 6
对于 2(5)，左1(1)，右4(2)，则(1, 4)之前高度都能达到5，面积为 5 * (4 - 1 - 1) = 10
对于 3(6)，左2(5)，右4(2)，则(2, 4)之前高度都能达到6，面积为 6 * (4 - 2 - 1) = 6
对于 4(2)，左1(1)，右6，则(1, 6)之前高度都能达到2，面积为 2 * (6 - 1 - 1) = 8
对于 5(3)，左4(2)，右6，则(4, 6)之前高度都能达到3，面积为 3 * (6 - 4 - 1) = 3

上述最大面积为10；

解题代码：

class Solution {
    public int largestRectangleArea(int[] heights) {
        Stack<Integer> s = new Stack<>(); // 存储元素索引，保持栈内元素索引对应的 heights 元素单调递增

        int n = heights.length;
        int max_area = 0;

        for(int i = 0; i < n; ++i){
            while(!s.isEmpty()){
                if(heights[s.peek()] > heights[i]){ // 栈顶元素大于当前元素，弹出栈顶元素
                    int idx = s.pop();
                    int pre = s.isEmpty() ? -1 : s.peek(); // 栈顶元素的左边第一个比它小的元素索引

                    max_area = Math.max(max_area, heights[idx] * (i - pre - 1)); // 计算以栈顶元素为高的矩形面积
                }else{
                    break;
                }
            }
            s.push(i);
        }

        // 栈里剩余元素，说明它们右边没有比它小的元素，r可记为n，也就是数组长度
        while(!s.isEmpty()){
            int idx = s.pop();
            int pre = s.isEmpty() ? -1 : s.peek(); // 栈顶元素的左边第一个比它小的元素索引

            max_area = Math.max(max_area, heights[idx] * (n - pre - 1)); // 计算以栈顶元素为高的矩形面积
        }

        return max_area;
    }
}

java